| 数据序列(1)元素数 | |
| 数据序列(2)元素数 | |
| (结果)数据元素数 |
CTRL+A :选中全部,CTRL+C:复制,CTRL+V:粘贴。 【使用必读】【本站支持微信扫码登录了】【除了计算器还有这些功能可用】
分类: 统计概率 标签:信号卷积公式 工具ID:915 阅读:15528 收藏
在输入框录入用空格、制表符、回车符或(英文半角)逗号隔开的数据序列(1)X(n)和数据序列(2)H(n)。点击计算按钮,本计算软件将快速求出输入序列元素的个数和卷积序列结果。
操作步骤:直接输入或复制记录表中的数据,粘贴到输入框,点击计算按钮,即可求出结果。输入多余的空格或分割符不影响计算结果。
例如:卷积计算题,已知X(n)=[5,4,3,2,1,1,2,3,4,5]和H(n)=[2,3,1,2],求其卷积?
计算结果:[10,23,23,27,19,13,12,15,21,29,25,13,10]
计算步骤:把两个序列像做乘法一样X列上、H列下,右端对齐。X列从右边第一个数5开始向左遍历,均乘以H列右侧第一个数2,这样得到一个新的数列,这个数列右端与H列中右端的2对齐,然后X列从右端开始向左遍历,每个数乘以H列中的1,也形成新的序列,这个序列右端与H列的1对齐。以此类推,形成四个序列,然后从上到下相加,就是最终结果。
卷积定义:
卷积是两个变量在某范围内相乘后求和的结果。如果卷积的变量是序列x(n)和h(n),则卷积的结果如下所示:
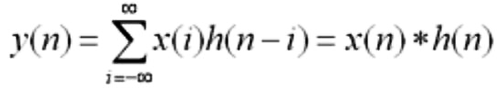
其中星号*表示卷积。当时序n=0时,序列h(-i)是h(i)的时序i取反的结果;时序取反使得h(i)以纵轴为中心翻转180度,所以这种相乘后求和的计算法称为卷积和,简称卷积。另外,n是使h(-i)位移的量,不同的n对应不同的卷积结果。
如果卷积的变量是函数x(t)和h(t),则卷积的计算变为下面公式:
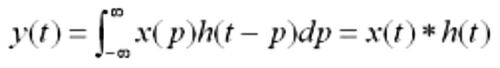
其中p是积分变量,积分也是求和,t是使函数h(-p)位移的量,星号*表示卷积。
卷积,互相关和自相关的视觉对比如下图所示:
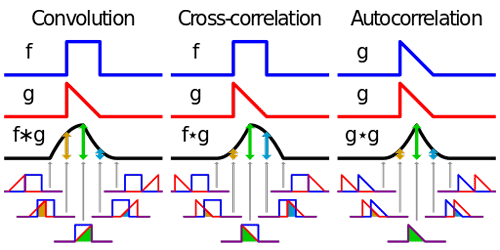
卷积定理指出,函数卷积的傅里叶变换是函数傅里叶变换的乘积。即,一个域中的卷积相当于另一个域中的乘积,例如时域中的卷积就对应于频域中的乘积。
F(g(x)*f(x))=F(g(x))F(f(x))
其中F表示的是傅里叶变换。
这一定理对拉普拉斯变换、双边拉普拉斯变换、Z变换、Mellin变换和Hartley变换(参见Mellininversiontheorem)等各种傅里叶变换的变体同样成立。在调和分析中还可以推广到在局部紧致的阿贝尔群上定义的傅里叶变换。
利用卷积定理可以简化卷积的运算量。对于长度为n的序列,按照卷积的定义进行计算,需要做2n-1组对位乘法,其计算复杂度为;而利用傅里叶变换将序列变换到频域上后,只需要一组对位乘法,利用傅里叶变换的快速算法之后,总的计算复杂度为。这一结果可以在快速乘法计算中得到应用。
相关推荐
信号卷积计算公式与在线计算器
在输入框录入用空格、制表符、回车符或(英文半角)逗号隔开的数据序列(1)X(n)和数据序列(2)H(n)。点击计算按钮,本计算软件将快速求出输入序列元素的个数和卷积序列结果。…
血浆渗透压(POP)计算公式(2)与在线计算器
输入血钠Na+(mmol/L) 、血钾K+(mmol/L)、血糖(mg/dL)、血尿素氮(mg/dL)等4个已知变量,点击计算按钮,可快速求出血浆渗透压(POP,mOsm/L)。血浆渗透压(POP)是…
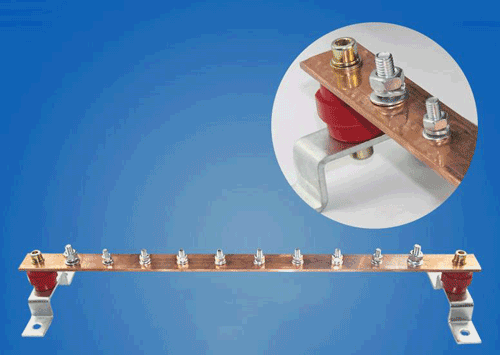
铜排的载流量计算公式(1)与在线计算器
在铜排设计过程中,我们一般是查询铜排的载流量表来确定铜排的载流值;严格来说,查表并不够精确,原因是铜排的载流能力与铜排的允许温升值有关,一般情况下,允许的温升值越高,那么电流密度可以越大。下面3种载流…
2023-04-12 21:49:48 | 分类:电子电路 | 阅读:20032 | 标签:铜排 载流量 计算公式 | 收藏
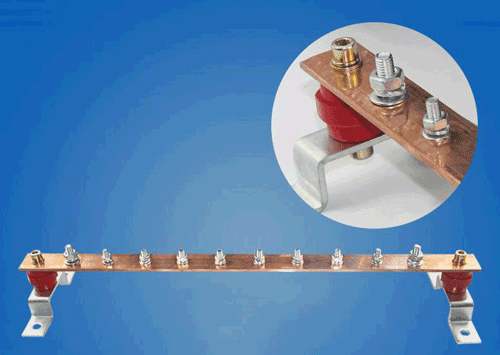
铜排的载流量计算公式(2)与在线计算器
在铜排设计过程中,我们一般是查询铜排的载流量表来确定铜排的载流值;严格来说,查表并不够精确,原因是铜排的载流能力与铜排的允许温升值有关,一般情况下,允许的温升值越高,那么电流密度可以越大。下面3种载流…
2023-04-12 21:55:13 | 分类:电子电路 | 阅读:3451 | 标签:铜排 载流量 计算公式 | 收藏
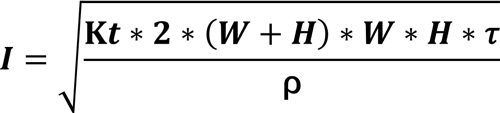
铜排的载流量计算公式(3)与在线计算器
在铜排设计过程中,我们一般是查询铜排的载流量表来确定铜排的载流值;严格来说,查表并不够精确,原因是铜排的载流能力与铜排的允许温升值有关,一般情况下,允许的温升值越高,那么电流密度可以越大。下面3种载流…
2023-04-12 21:56:19 | 分类:电子电路 | 阅读:9247 | 标签:铜排 载流量 计算公式 | 收藏
- 分类
- 校验计算 29
- 文字处理 10
- 电子电路 100
- 颜色计算 6
- 时间日期 18
- 数学计算 17
- 统计概率 58
- 方程代数 24
- 复数向量 15
- 对数分数 30
- 指数开方 9
- 平面几何 34
- 物理计算 52
- 立体几何 53
- 工程设计 219
- 材料报价 40
- 标准规程 8
- 单位转换 42
- 生活健康 137
- 金融理财 37
- 其他工具 8
- 进制数字 26
- 代码工具 29
- 三角函数 13
- 点阵字模 17
- 位运算 4
- 矩阵多项式 22
- 使用榜
- 1. 原码,反码,补码相互转换在线计算器
- 2. ppm,mg/m^3,ug/m^3气体浓度单位转换在线计算器
- 3. 圆柱形罐体(卧式圆筒)剩余液体积,容积及质量在线计算器
- 4. (一元二次)方程求解在线计算器
- 5. 英寸,码,英尺,毫米,厘米,米单位转换在线计算器
- 6. mil,mm,in,cm单位转换在线计算器
- 7. 16进制(CRC16)(累加和),ASCII码校验和在线计算器
- 8. 16进制(单精度,双精度,浮点数)转10进制,IEEE-754标准浮点数在线计算器
- 9. 交集A∩B,并集A∪B集合在线计算器
- 10. 气体流量(m3/h,kmol/h,CFM,L/min)等单位转换在线计算器
