| 数据序列元素数 | |
| 最值(min,max) | |
| 范围(max-min) | |
| 平均值(mean) | |
| (样本)标准偏差(SD) | |
| (总体)标准偏差(SD) |
CTRL+A :选中全部,CTRL+C:复制,CTRL+V:粘贴。 【使用必读】【本站支持微信扫码登录了】【除了计算器还有这些功能可用】
分类: 统计概率 标签:频率分布排序平均值标准偏差 工具ID:955 阅读:5073 收藏
输入用空格、制表符、回车符或(英文半角)逗号隔开的数据序列后点击计算,可求其正反序、算术平均数、(样本)均方根标准偏差(SD)、(总体)均方根标准偏差(SD)、频率分布等结果。
标准差(Standard Deviation),标准差是方差的算术平方根,也称均方差(mean square error),是各数据偏离平均数的距离的平均数,它是离均差平方和平均后的方根,用σ表示,标准差能反映一个数据集的离散程度。
操作步骤:直接输入或复制记录表中的数据,粘贴到输入框,点击计算按钮,即可求出结果。输入多余的空格或分割符不影响计算结果。
样本标准差和总体标准差的区别是什么?计算上有什么不同?
样本标准差=√[1/(n-1)Σ(Xi-/X)²] i从1到n
总体标准差=√ {∫[-∞→+∞] (x-E(X))²f(x) dx} f(x)是总体的概率密度,E(X)是总体的期望。
如是总体,标准差公式根号内除以n
如是样本,标准差公式根号内除以(n-1)
样本的标准差是用数据算出来的,只要有测量数据就可以计算,而总体的标准差要通过概率密度才能求出来,一般是做不到的。样本的标准差是总体标准差的近似。
故一般取(样本)校标准差作为计算结果。
两者计算公式如下:
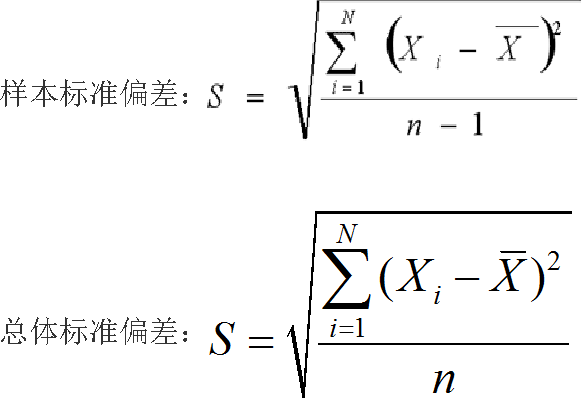
相关推荐

加权平均值与算数平均值在线计算器
在数据输入框和权重输入框录入用空格、制表符、回车符或(英文半角)逗号隔开的数值。点击计算按钮,可快速求出其,数值算数和、算数平均值、数值加权和(分子)、权重和(分母)、加权平均值等结果。…
2019-01-30 23:01:46 | 分类:统计概率 | 阅读:35585 | 标签:加权平均值 算数平均值 | 收藏
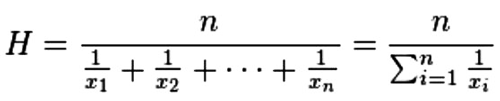
谐波平均值(Harmonic Mean)计算公式与在线计算器
在输入框录入用空格、制表符、回车符或(英文半角)逗号隔开的数据序列X。点击计算按钮,本计算软件将快速求出输入序列元素的个数、谐波平均值H等结果。…
2020-03-15 21:57:18 | 分类:统计概率 | 阅读:1817 | 标签:谐波均值 Harmonic Mean | 收藏

分组算术平均值(Group Arithmetic Mean)计算公式与在线计算器
在输入框录入用空格、制表符、回车符或(英文半角)逗号隔开的数据序列X(数值)和数据序列Y(频率分布)。点击计算按钮,本计算软件将快速求出输入序列元素的个数、分组算术平均值M等结果。…
2020-03-15 22:54:06 | 分类:统计概率 | 阅读:2068 | 标签:分组 算术 平均值 Group Arithmetic Mean | 收藏
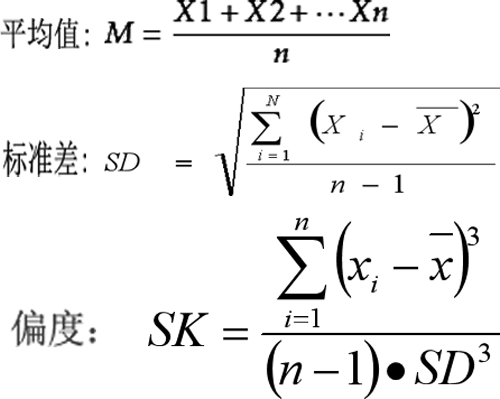
平均值,标准差,偏度(skewness)计算公式与在线计算器
在输入框录入用空格、制表符、回车符或(英文半角)逗号隔开的数据序列X。点击计算按钮,本计算软件将快速求出输入序列元素的个数、平均值(M)、标准差(SD)、中间变量Sum(xi -/x)^3、偏度(SK…
2020-03-16 21:19:23 | 分类:统计概率 | 阅读:20012 | 标签:平均值 标准差 偏度 | 收藏
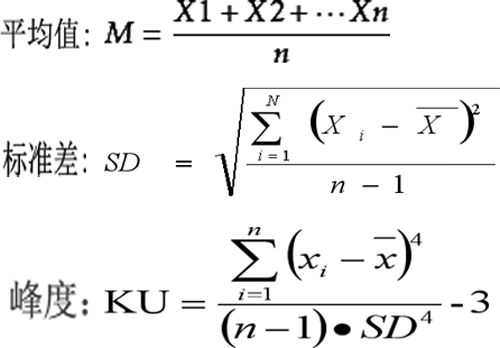
平均值,标准差,峰度(Kurtosis)计算公式与在线计算器
在输入框录入用空格、制表符、回车符或(英文半角)逗号隔开的数据序列X。点击计算按钮,本计算软件将快速求出输入序列元素的个数、平均值(M)、标准差(SD)、中间变量Sum(xi -/x)^4、峰度(KU…
2020-03-16 22:24:53 | 分类:统计概率 | 阅读:8664 | 标签:平均值 标准差 峰度 | 收藏
已知平均值标准差求置信区间计算公式与在线计算器
输入置信水平、样本量(n)、平均值(x)、样本标准差(σ)等已知量,点击计算按钮,可快速求出给定输入的置信区间。…
- 分类
- 校验计算 29
- 文字处理 10
- 电子电路 100
- 颜色计算 6
- 时间日期 18
- 数学计算 17
- 统计概率 58
- 方程代数 24
- 复数向量 15
- 对数分数 30
- 指数开方 9
- 平面几何 34
- 物理计算 52
- 立体几何 53
- 工程设计 219
- 材料报价 40
- 标准规程 8
- 单位转换 42
- 生活健康 137
- 金融理财 37
- 其他工具 8
- 进制数字 26
- 代码工具 29
- 三角函数 13
- 点阵字模 17
- 位运算 4
- 矩阵多项式 22
- 使用榜
- 1. 16进制(CRC16)(MODBUS RTU通讯)校验码在线计算器
- 2. 赫兹Hz,秒s等常见频率,周期单位转换在线计算器
- 3. 椭圆封头储罐(卧式)液位对应体积计算公式与在线计算器
- 4. 16进制(CRC8)(累加和,LRC校验),ASCII码校验和在线计算器
- 5. 电阻分压在线计算器
- 6. 圆柱形罐体(卧式圆筒)剩余液体积,容积及质量在线计算器
- 7. 10进制(单精度,双精度,浮点数)转16进制,IEEE-754标准浮点数在线计算器
- 8. 长方体货物(包装箱)总体积,总重量在线计算器
- 9. 电容容抗,电容与频率计算公式与在线计算器
- 10. 企业(销售毛利率)计算公式与在线计算器