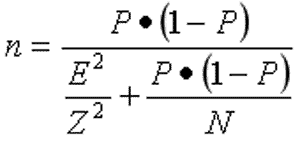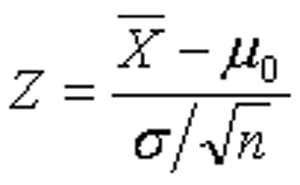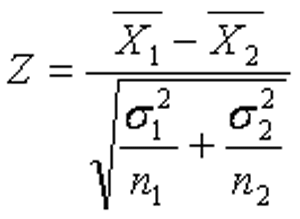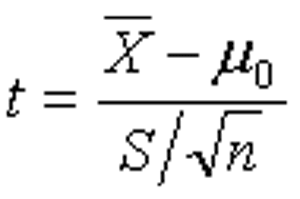| 样本数(1) | |
| 样本数(2) | |
| 平均数(/X1) | |
| 平均数(/X2) | |
| (结果)Z检验(Z-test) |
CTRL+A :选中全部,CTRL+C:复制,CTRL+V:粘贴。 【使用必读】【本站支持微信扫码登录了】【除了计算器还有这些功能可用】
分类: 统计概率 标签:显着性差异Z检验Z-TEST比较总体均值常数显着性差异 工具ID:1044 阅读:1863 收藏
输入样本数据(1)、样本数据(2)(应以空格、逗号(半角)、回车或制表符(Tab)隔开)、总体标准差σ1和总体标准差σ2等已知参数,点击计算按钮,可快速求出Z检验(Z-TEST)结果。
1.Z分布即为 正态分布 (normal distribution)。
正态分布的两个参数μ和σ决定了正态分布的位置和形态。为了应用方便,常将一般的正态变量X通过u变换[(X-μ)/σ]转化成标准正态变量Z,以使原来各种形态的正态分布都转换为μ=0,σ=1的标准正态分布(standard normaldistribution),亦称Z分布。
根据中心极限定理,通过抽样模拟试验表明,在正态分布总体中以固定 n 抽取若干个样本时,样本均数的分布仍服从正态分布,即N(μ,σ)。所以,对样本均数的分布进行Z变换,也可变换为标准正态分布N (0,1) 。
正态分布的概率密度函数为:

其图像如下:

2.适用条件
- 正态分布
- 总体标准差已知或者样本容量足够大(>30)
3. 用途
- 检验一个样本平均数与一个己知的总体平均数的差异是否显着
- 检验来自两个的两组样本平均数的差异性,从而判断它们各自代表的总体的差异是否显着
4.公式
- 公式一:总体标准差已知或样本容量大于30,比较某个总体的均值与某个常数是否有显着性的差异,检验公式如下:

其中, /X 为样本均值, μ 0 为总体均值, σ 为总体标准差, n为样本容量。
- 公式二:总体标准差已知或样本容量大于30,比较两个总体的均值是否有显着性的差异,检验公式如下:

相关推荐
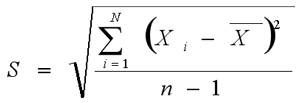
平均值,样本标准差,总体标准偏差计算公式与在线计算器
输入用空格、制表符、回车符或(英文半角)逗号隔开的测量值(Xi)后点击计算,可求其算术平均数与均方根标准偏差(S)。标准差(Standard Deviation),标准差是方差的算术平方根,也称均方差…

谐波平均值(Harmonic Mean)计算公式与在线计算器
在输入框录入用空格、制表符、回车符或(英文半角)逗号隔开的数据序列X。点击计算按钮,本计算软件将快速求出输入序列元素的个数、谐波平均值H等结果。…
2020-03-15 21:57:18 | 分类:统计概率 | 阅读:1805 | 标签:谐波均值 Harmonic Mean | 收藏

分组算术平均值(Group Arithmetic Mean)计算公式与在线计算器
在输入框录入用空格、制表符、回车符或(英文半角)逗号隔开的数据序列X(数值)和数据序列Y(频率分布)。点击计算按钮,本计算软件将快速求出输入序列元素的个数、分组算术平均值M等结果。…
2020-03-15 22:54:06 | 分类:统计概率 | 阅读:2058 | 标签:分组 算术 平均值 Group Arithmetic Mean | 收藏

平均值,标准差,峰度(Kurtosis)计算公式与在线计算器
在输入框录入用空格、制表符、回车符或(英文半角)逗号隔开的数据序列X。点击计算按钮,本计算软件将快速求出输入序列元素的个数、平均值(M)、标准差(SD)、中间变量Sum(xi -/x)^4、峰度(KU…
2020-03-16 22:24:53 | 分类:统计概率 | 阅读:8635 | 标签:平均值 标准差 峰度 | 收藏
平均值,中位数,众数计算公式与在线计算器
输入数据序列X,点击计算按钮,可快速求出数据序列元素数N、平均值M、中位数MD、众数(Mode)等结果。众数(Mode)是统计学名词,在统计分布上具有明显集中趋势点的数值,代表数据的一般水平(众数可以…
2020-03-20 21:17:56 | 分类:统计概率 | 阅读:23045 | 标签:平均值 中位数 众数 | 收藏
- 分类
- 校验计算 29
- 文字处理 10
- 电子电路 100
- 颜色计算 6
- 时间日期 18
- 数学计算 17
- 统计概率 58
- 方程代数 24
- 复数向量 15
- 对数分数 30
- 指数开方 9
- 平面几何 34
- 物理计算 52
- 立体几何 53
- 工程设计 219
- 材料报价 40
- 标准规程 8
- 单位转换 42
- 生活健康 137
- 金融理财 37
- 其他工具 8
- 进制数字 26
- 代码工具 29
- 三角函数 13
- 点阵字模 17
- 位运算 4
- 矩阵多项式 22
- 使用榜
- 1. 16进制(单精度,双精度,浮点数)转10进制,IEEE-754标准浮点数在线计算器
- 2. GFR肾小球滤过率(MDRD)计算公式与在线计算器
- 3. 椭圆封头储罐(卧式)液位对应体积计算公式与在线计算器
- 4. GFR肾小球滤过率(CKD-EPI)计算公式与在线计算器
- 5. 16进制(CRC16)(累加和),ASCII码校验和在线计算器
- 6. 直角三角形面积,周长,夹角,勾股定理,毕达哥拉斯在线计算器
- 7. 16进制(CRC16)(MODBUS RTU通讯)校验码在线计算器
- 8. 位运算(按位左移,右移)在线计算器
- 9. 圆柱形罐体(卧式圆筒)剩余液体积,容积及质量在线计算器
- 10. 原码,反码,补码相互转换在线计算器